Theorem fun11iun 5147

Description: The union of a chain (with respect to inclusion) of one-to-one functions is a one-to-one function. (Contributed by Mario Carneiro, 20-May-2013.) (Revised by Mario Carneiro, 24-Jun-2015.)

Hypotheses

Ref	Expression
fun11iun.1	|- ( x = y -> B = C )
fun11iun.2	|- B e. _V

Assertion

Ref	Expression
fun11iun	|- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> U_ x e. A B : U_ x e. A D -1-1-> S )

Distinct variable groups:   x, A   y, A   y, B   x, C   x, S

Allowed substitution hints:   B( x)   C( y)   D( x, y)   S( y)

Proof of Theorem fun11iun

Dummy variables u v z are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		vex 2560	. . . . . . . . . 10 |- u e. _V
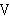2		eqeq1 2046	. . . . . . . . . . 11 |- ( z = u -> ( z = B <-> u = B ) )
3	2	rexbidv 2327	. . . . . . . . . 10 |- ( z = u -> ( E. x e. A z = B <-> E. x e. A u = B ) )
4	1, 3	elab 2687	. . . . . . . . 9 |- ( u e. { z | E. x e. A z = B } <-> E. x e. A u = B )
5		r19.29 2450	. . . . . . . . . 10 |- ( ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ E. x e. A u = B ) -> E. x e. A ( ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ u = B ) )
6		nfv 1421	. . . . . . . . . . . 12 |- F/ x ( Fun u /\ Fun `' u )
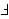
7		nfre1 2365	. . . . . . . . . . . . . 14 |- F/ x E. x e. A z = B
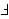
8	7	nfab 2182	. . . . . . . . . . . . 13 |- F/_ x { z | E. x e. A z = B }
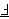
9		nfv 1421	. . . . . . . . . . . . 13 |- F/ x ( u C_ v \/ v C_ u )
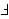
10	8, 9	nfralxy 2360	. . . . . . . . . . . 12 |- F/ x A. v e. { z | E. x e. A z = B } ( u C_ v \/ v C_ u )
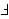
11	6, 10	nfan 1457	. . . . . . . . . . 11 |- F/ x ( ( Fun u /\ Fun `' u ) /\ A. v e. { z | E. x e. A z = B } ( u C_ v \/ v C_ u ) )
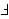
12		f1eq1 5087	. . . . . . . . . . . . . . . 16 |- ( u = B -> ( u : D -1-1-> S <-> B : D -1-1-> S ) )
13	12	biimparc 283	. . . . . . . . . . . . . . 15 |- ( ( B : D -1-1-> S /\ u = B ) -> u : D -1-1-> S )
14		df-f1 4907	. . . . . . . . . . . . . . . 16 |- ( u : D -1-1-> S <-> ( u : D --> S /\ Fun `' u ) )
15		ffun 5048	. . . . . . . . . . . . . . . . 17 |- ( u : D --> S -> Fun u )
16	15	anim1i 323	. . . . . . . . . . . . . . . 16 |- ( ( u : D --> S /\ Fun `' u ) -> ( Fun u /\ Fun `' u ) )
17	14, 16	sylbi 114	. . . . . . . . . . . . . . 15 |- ( u : D -1-1-> S -> ( Fun u /\ Fun `' u ) )
18	13, 17	syl 14	. . . . . . . . . . . . . 14 |- ( ( B : D -1-1-> S /\ u = B ) -> ( Fun u /\ Fun `' u ) )
19	18	adantlr 446	. . . . . . . . . . . . 13 |- ( ( ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ u = B ) -> ( Fun u /\ Fun `' u ) )
20		vex 2560	. . . . . . . . . . . . . . . 16 |- v e. _V
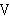21		eqeq1 2046	. . . . . . . . . . . . . . . . 17 |- ( z = v -> ( z = B <-> v = B ) )
22	21	rexbidv 2327	. . . . . . . . . . . . . . . 16 |- ( z = v -> ( E. x e. A z = B <-> E. x e. A v = B ) )
23	20, 22	elab 2687	. . . . . . . . . . . . . . 15 |- ( v e. { z | E. x e. A z = B } <-> E. x e. A v = B )
24		fun11iun.1	. . . . . . . . . . . . . . . . . 18 |- ( x = y -> B = C )
25	24	eqeq2d 2051	. . . . . . . . . . . . . . . . 17 |- ( x = y -> ( v = B <-> v = C ) )
26	25	cbvrexv 2534	. . . . . . . . . . . . . . . 16 |- ( E. x e. A v = B <-> E. y e. A v = C )
27		r19.29 2450	. . . . . . . . . . . . . . . . . . 19 |- ( ( A. y e. A ( B C_ C \/ C C_ B ) /\ E. y e. A v = C ) -> E. y e. A ( ( B C_ C \/ C C_ B ) /\ v = C ) )
28		sseq12 2968	. . . . . . . . . . . . . . . . . . . . . . . . 25 |- ( ( u = B /\ v = C ) -> ( u C_ v <-> B C_ C ) )
29	28	ancoms 255	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( ( v = C /\ u = B ) -> ( u C_ v <-> B C_ C ) )
30		sseq12 2968	. . . . . . . . . . . . . . . . . . . . . . . 24 |- ( ( v = C /\ u = B ) -> ( v C_ u <-> C C_ B ) )
31	29, 30	orbi12d 707	. . . . . . . . . . . . . . . . . . . . . . 23 |- ( ( v = C /\ u = B ) -> ( ( u C_ v \/ v C_ u ) <-> ( B C_ C \/ C C_ B ) ) )
32	31	biimprcd 149	. . . . . . . . . . . . . . . . . . . . . 22 |- ( ( B C_ C \/ C C_ B ) -> ( ( v = C /\ u = B ) -> ( u C_ v \/ v C_ u ) ) )
33	32	expdimp 246	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( ( B C_ C \/ C C_ B ) /\ v = C ) -> ( u = B -> ( u C_ v \/ v C_ u ) ) )
34	33	rexlimivw 2429	. . . . . . . . . . . . . . . . . . . 20 |- ( E. y e. A ( ( B C_ C \/ C C_ B ) /\ v = C ) -> ( u = B -> ( u C_ v \/ v C_ u ) ) )
35	34	imp 115	. . . . . . . . . . . . . . . . . . 19 |- ( ( E. y e. A ( ( B C_ C \/ C C_ B ) /\ v = C ) /\ u = B ) -> ( u C_ v \/ v C_ u ) )
36	27, 35	sylan 267	. . . . . . . . . . . . . . . . . 18 |- ( ( ( A. y e. A ( B C_ C \/ C C_ B ) /\ E. y e. A v = C ) /\ u = B ) -> ( u C_ v \/ v C_ u ) )
37	36	an32s 502	. . . . . . . . . . . . . . . . 17 |- ( ( ( A. y e. A ( B C_ C \/ C C_ B ) /\ u = B ) /\ E. y e. A v = C ) -> ( u C_ v \/ v C_ u ) )
38	37	adantlll 449	. . . . . . . . . . . . . . . 16 |- ( ( ( ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ u = B ) /\ E. y e. A v = C ) -> ( u C_ v \/ v C_ u ) )
39	26, 38	sylan2b 271	. . . . . . . . . . . . . . 15 |- ( ( ( ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ u = B ) /\ E. x e. A v = B ) -> ( u C_ v \/ v C_ u ) )
40	23, 39	sylan2b 271	. . . . . . . . . . . . . 14 |- ( ( ( ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ u = B ) /\ v e. { z | E. x e. A z = B } ) -> ( u C_ v \/ v C_ u ) )
41	40	ralrimiva 2392	. . . . . . . . . . . . 13 |- ( ( ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ u = B ) -> A. v e. { z | E. x e. A z = B } ( u C_ v \/ v C_ u ) )
42	19, 41	jca 290	. . . . . . . . . . . 12 |- ( ( ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ u = B ) -> ( ( Fun u /\ Fun `' u ) /\ A. v e. { z | E. x e. A z = B } ( u C_ v \/ v C_ u ) ) )
43	42	a1i 9	. . . . . . . . . . 11 |- ( x e. A -> ( ( ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ u = B ) -> ( ( Fun u /\ Fun `' u ) /\ A. v e. { z | E. x e. A z = B } ( u C_ v \/ v C_ u ) ) ) )
44	11, 43	rexlimi 2426	. . . . . . . . . 10 |- ( E. x e. A ( ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ u = B ) -> ( ( Fun u /\ Fun `' u ) /\ A. v e. { z | E. x e. A z = B } ( u C_ v \/ v C_ u ) ) )
45	5, 44	syl 14	. . . . . . . . 9 |- ( ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ E. x e. A u = B ) -> ( ( Fun u /\ Fun `' u ) /\ A. v e. { z | E. x e. A z = B } ( u C_ v \/ v C_ u ) ) )
46	4, 45	sylan2b 271	. . . . . . . 8 |- ( ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ u e. { z | E. x e. A z = B } ) -> ( ( Fun u /\ Fun `' u ) /\ A. v e. { z | E. x e. A z = B } ( u C_ v \/ v C_ u ) ) )
47	46	ralrimiva 2392	. . . . . . 7 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> A. u e. { z | E. x e. A z = B } ( ( Fun u /\ Fun `' u ) /\ A. v e. { z | E. x e. A z = B } ( u C_ v \/ v C_ u ) ) )
48		fun11uni 4969	. . . . . . 7 |- ( A. u e. { z | E. x e. A z = B } ( ( Fun u /\ Fun `' u ) /\ A. v e. { z | E. x e. A z = B } ( u C_ v \/ v C_ u ) ) -> ( Fun U. { z | E. x e. A z = B } /\ Fun `' U. { z | E. x e. A z = B } ) )
49	47, 48	syl 14	. . . . . 6 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> ( Fun U. { z | E. x e. A z = B } /\ Fun `' U. { z | E. x e. A z = B } ) )
50	49	simpld 105	. . . . 5 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> Fun U. { z | E. x e. A z = B } )
51		fun11iun.2	. . . . . . 7 |- B e. _V
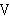52	51	dfiun2 3691	. . . . . 6 |- U_ x e. A B = U. { z | E. x e. A z = B }
53	52	funeqi 4922	. . . . 5 |- ( Fun U_ x e. A B <-> Fun U. { z | E. x e. A z = B } )
54	50, 53	sylibr 137	. . . 4 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> Fun U_ x e. A B )
55		nfra1 2355	. . . . . . 7 |- F/ x A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) )
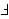
56		rsp 2369	. . . . . . . . 9 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> ( x e. A -> ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) ) )
57	1	eldm2 4533	. . . . . . . . . . 11 |- ( u e. dom B <-> E. v <. u , v >. e. B )
58		f1dm 5096	. . . . . . . . . . . 12 |- ( B : D -1-1-> S -> dom B = D )
59	58	eleq2d 2107	. . . . . . . . . . 11 |- ( B : D -1-1-> S -> ( u e. dom B <-> u e. D ) )
60	57, 59	syl5bbr 183	. . . . . . . . . 10 |- ( B : D -1-1-> S -> ( E. v <. u , v >. e. B <-> u e. D ) )
61	60	adantr 261	. . . . . . . . 9 |- ( ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> ( E. v <. u , v >. e. B <-> u e. D ) )
62	56, 61	syl6 29	. . . . . . . 8 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> ( x e. A -> ( E. v <. u , v >. e. B <-> u e. D ) ) )
63	62	imp 115	. . . . . . 7 |- ( ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) /\ x e. A ) -> ( E. v <. u , v >. e. B <-> u e. D ) )
64	55, 63	rexbida 2321	. . . . . 6 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> ( E. x e. A E. v <. u , v >. e. B <-> E. x e. A u e. D ) )
65		eliun 3661	. . . . . . . 8 |- ( <. u , v >. e. U_ x e. A B <-> E. x e. A <. u , v >. e. B )
66	65	exbii 1496	. . . . . . 7 |- ( E. v <. u , v >. e. U_ x e. A B <-> E. v E. x e. A <. u , v >. e. B )
67	1	eldm2 4533	. . . . . . 7 |- ( u e. dom U_ x e. A B <-> E. v <. u , v >. e. U_ x e. A B )
68		rexcom4 2577	. . . . . . 7 |- ( E. x e. A E. v <. u , v >. e. B <-> E. v E. x e. A <. u , v >. e. B )
69	66, 67, 68	3bitr4i 201	. . . . . 6 |- ( u e. dom U_ x e. A B <-> E. x e. A E. v <. u , v >. e. B )
70		eliun 3661	. . . . . 6 |- ( u e. U_ x e. A D <-> E. x e. A u e. D )
71	64, 69, 70	3bitr4g 212	. . . . 5 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> ( u e. dom U_ x e. A B <-> u e. U_ x e. A D ) )
72	71	eqrdv 2038	. . . 4 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> dom U_ x e. A B = U_ x e. A D )
73		df-fn 4905	. . . 4 |- ( U_ x e. A B Fn U_ x e. A D <-> ( Fun U_ x e. A B /\ dom U_ x e. A B = U_ x e. A D ) )
74	54, 72, 73	sylanbrc 394	. . 3 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> U_ x e. A B Fn U_ x e. A D )
75		rniun 4734	. . . 4 |- ran U_ x e. A B = U_ x e. A ran B
76		f1f 5092	. . . . . . . 8 |- ( B : D -1-1-> S -> B : D --> S )
77		frn 5052	. . . . . . . 8 |- ( B : D --> S -> ran B C_ S )
78	76, 77	syl 14	. . . . . . 7 |- ( B : D -1-1-> S -> ran B C_ S )
79	78	adantr 261	. . . . . 6 |- ( ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> ran B C_ S )
80	79	ralimi 2384	. . . . 5 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> A. x e. A ran B C_ S )
81		iunss 3698	. . . . 5 |- ( U_ x e. A ran B C_ S <-> A. x e. A ran B C_ S )
82	80, 81	sylibr 137	. . . 4 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> U_ x e. A ran B C_ S )
83	75, 82	syl5eqss 2989	. . 3 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> ran U_ x e. A B C_ S )
84		df-f 4906	. . 3 |- ( U_ x e. A B : U_ x e. A D --> S <-> ( U_ x e. A B Fn U_ x e. A D /\ ran U_ x e. A B C_ S ) )
85	74, 83, 84	sylanbrc 394	. 2 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> U_ x e. A B : U_ x e. A D --> S )
86	49	simprd 107	. . 3 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> Fun `' U. { z | E. x e. A z = B } )
87	52	cnveqi 4510	. . . 4 |- `' U_ x e. A B = `' U. { z | E. x e. A z = B }
88	87	funeqi 4922	. . 3 |- ( Fun `' U_ x e. A B <-> Fun `' U. { z | E. x e. A z = B } )
89	86, 88	sylibr 137	. 2 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> Fun `' U_ x e. A B )
90		df-f1 4907	. 2 |- ( U_ x e. A B : U_ x e. A D -1-1-> S <-> ( U_ x e. A B : U_ x e. A D --> S /\ Fun `' U_ x e. A B ) )
91	85, 89, 90	sylanbrc 394	1 |- ( A. x e. A ( B : D -1-1-> S /\ A. y e. A ( B C_ C \/ C C_ B ) ) -> U_ x e. A B : U_ x e. A D -1-1-> S )

Syntax hints:   -> wi 4   /\ wa 97   <-> wb 98   \/ wo 629   = wceq 1243   E.wex 1381   e. wcel 1393   {cab 2026   A.wral 2306   E.wrex 2307   _Vcvv 2557   C_ wss 2917   <.cop 3378   U.cuni 3580   U_ciun 3657   `'ccnv 4344   dom cdm 4345   ran crn 4346   Fun wfun 4896   Fn wfn 4897   -->wf 4898   -1-1->wf1 4899

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 99  ax-ia2 100  ax-ia3 101  ax-io 630  ax-5 1336  ax-7 1337  ax-gen 1338  ax-ie1 1382  ax-ie2 1383  ax-8 1395  ax-10 1396  ax-11 1397  ax-i12 1398  ax-bndl 1399  ax-4 1400  ax-13 1404  ax-14 1405  ax-17 1419  ax-i9 1423  ax-ial 1427  ax-i5r 1428  ax-ext 2022  ax-sep 3875  ax-pow 3927  ax-pr 3944  ax-un 4170

This theorem depends on definitions:  df-bi 110  df-3an 887  df-tru 1246  df-nf 1350  df-sb 1646  df-eu 1903  df-mo 1904  df-clab 2027  df-cleq 2033  df-clel 2036  df-nfc 2167  df-ral 2311  df-rex 2312  df-v 2559  df-un 2922  df-in 2924  df-ss 2931  df-pw 3361  df-sn 3381  df-pr 3382  df-op 3384  df-uni 3581  df-iun 3659  df-br 3765  df-opab 3819  df-id 4030  df-xp 4351  df-rel 4352  df-cnv 4353  df-co 4354  df-dm 4355  df-rn 4356  df-fun 4904  df-fn 4905  df-f 4906  df-f1 4907

This theorem is referenced by: (None)