| Step | Hyp | Ref
| Expression |
|---|
| 1 | | df-enq0 6522 |
. . 3
 ~Q0
~Q0                   
                                                 |
| 2 | | df-xp 4351 |
. . 3
                                        |
| 3 | 1, 2 | ineq12i 3136 |
. 2
  ~Q0 ~Q0
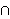                                  
                                                 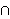                           |
| 4 | | inopab 4468 |
. 2
                 
                                                   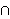                                  
           
                                                        
           |
| 5 | | an32 496 |
. . . . . 6
                     
                                                
          
           
                                                                    |
| 6 | | an4 520 |
. . . . . . . 8
            
                          
                                      |
| 7 | | pinn 6407 |
. . . . . . . . . . . . 13
          |
| 8 | 7 | ssriv 2949 |
. . . . . . . . . . . 12
    |
| 9 | | xpss1 4448 |
. . . . . . . . . . . 12
     
            |
| 10 | 8, 9 | ax-mp 7 |
. . . . . . . . . . 11
            |
| 11 | 10 | sseli 2941 |
. . . . . . . . . 10
        
         |
| 12 | 11 | pm4.71ri 372 |
. . . . . . . . 9
        
                   |
| 13 | 10 | sseli 2941 |
. . . . . . . . . 10
        
         |
| 14 | 13 | pm4.71ri 372 |
. . . . . . . . 9
        
                   |
| 15 | 12, 14 | anbi12i 433 |
. . . . . . . 8
                   
                                      |
| 16 | 6, 15 | bitr4i 176 |
. . . . . . 7
            
                          
                  |
| 17 | 16 | anbi1i 431 |
. . . . . 6
                     
                                                                    
                                                   |
| 18 | 5, 17 | bitri 173 |
. . . . 5
                     
                                                
          
                                                            |
| 19 | | eleq1 2100 |
. . . . . . . . . . . . . . . . . . 19
                                |
| 20 | | opelxp 4374 |
. . . . . . . . . . . . . . . . . . 19
                        |
| 21 | 19, 20 | syl6bb 185 |
. . . . . . . . . . . . . . . . . 18
                              |
| 22 | | eleq1 2100 |
. . . . . . . . . . . . . . . . . . 19
                                |
| 23 | | opelxp 4374 |
. . . . . . . . . . . . . . . . . . 19
                        |
| 24 | 22, 23 | syl6bb 185 |
. . . . . . . . . . . . . . . . . 18
                              |
| 25 | 21, 24 | bi2anan9 538 |
. . . . . . . . . . . . . . . . 17
         
         
                  
       
               |
| 26 | 25 | pm5.32i 427 |
. . . . . . . . . . . . . . . 16
                            
          
        
                 
               |
| 27 | 26 | anbi1i 431 |
. . . . . . . . . . . . . . 15
                                                                               
   
       
                  |
| 28 | | anass 381 |
. . . . . . . . . . . . . . 15
                                                         
        
                                
              |
| 29 | 27, 28 | bitri 173 |
. . . . . . . . . . . . . 14
                                                                               
   
       
   
              |
| 30 | | mulpiord 6415 |
. . . . . . . . . . . . . . . . . 18
        
               |
| 31 | | mulpiord 6415 |
. . . . . . . . . . . . . . . . . 18
        
               |
| 32 | 30, 31 | eqeqan12d 2055 |
. . . . . . . . . . . . . . . . 17
                       
            
             |
| 33 | 32 | an42s 523 |
. . . . . . . . . . . . . . . 16
                       
            
             |
| 34 | 33 | pm5.32i 427 |
. . . . . . . . . . . . . . 15
        
   
       
   
                     
             
             |
| 35 | 34 | anbi2i 430 |
. . . . . . . . . . . . . 14
                                           
             
        
                                
              |
| 36 | 29, 35 | bitr4i 176 |
. . . . . . . . . . . . 13
                                                                               
   
       
   
              |
| 37 | | anass 381 |
. . . . . . . . . . . . 13
                                                         
        
                                
              |
| 38 | 36, 37 | bitr4i 176 |
. . . . . . . . . . . 12
                                                                               
   
       
                  |
| 39 | 26 | anbi1i 431 |
. . . . . . . . . . . 12
                                                                               
   
       
                  |
| 40 | 38, 39 | bitr4i 176 |
. . . . . . . . . . 11
                                                                                   
                      |
| 41 | | ancom 253 |
. . . . . . . . . . . 12
                            
          
                          
           |
| 42 | 41 | anbi1i 431 |
. . . . . . . . . . 11
                                                               
                 
                        |
| 43 | 41 | anbi1i 431 |
. . . . . . . . . . 11
                                                               
                 
                        |
| 44 | 40, 42, 43 | 3bitr3i 199 |
. . . . . . . . . 10
                     
                  
                                        
                        |
| 45 | | anass 381 |
. . . . . . . . . 10
                     
                  
                     
                                           |
| 46 | | anass 381 |
. . . . . . . . . 10
                     
                  
                     
                                           |
| 47 | 44, 45, 46 | 3bitr3i 199 |
. . . . . . . . 9
            
                                                 
                                           |
| 48 | 47 | 2exbii 1497 |
. . . . . . . 8
                
                                                               
        
                        |
| 49 | | 19.42vv 1788 |
. . . . . . . 8
                
                                                 
                      
                        |
| 50 | | 19.42vv 1788 |
. . . . . . . 8
                
                                                 
                      
                        |
| 51 | 48, 49, 50 | 3bitr3i 199 |
. . . . . . 7
            
                                                     
                      
                        |
| 52 | 51 | 2exbii 1497 |
. . . . . 6
                
                                                                   
                                     |
| 53 | | 19.42vv 1788 |
. . . . . 6
                
                                                     
                                                   |
| 54 | | 19.42vv 1788 |
. . . . . 6
                
                                                     
                                                   |
| 55 | 52, 53, 54 | 3bitr3i 199 |
. . . . 5
            
                                                         
                                                   |
| 56 | 18, 55 | bitri 173 |
. . . 4
                     
                                                
          
                                                            |
| 57 | 56 | opabbii 3824 |
. . 3
                           
                                                
                             
                                                 |
| 58 | | df-enq 6445 |
. . 3
         
                                                            |
| 59 | 57, 58 | eqtr4i 2063 |
. 2
                           
                                                
             |
| 60 | 3, 4, 59 | 3eqtrri 2065 |
1
    ~Q0 ~Q0 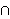      
        |