| Step | Hyp | Ref
| Expression |
|---|
| 1 | | enq0er 6533 |
. . . . . . . . . . . . . 14
 ~Q0
~Q0       |
| 2 | 1 | a1i 9 |
. . . . . . . . . . . . 13
             ~Q0 ~Q0            ~Q0 ~Q0               ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0             ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0     ~Q0
~Q0        |
| 3 | | nnnq0lem1 6544 |
. . . . . . . . . . . . . 14
             ~Q0 ~Q0            ~Q0 ~Q0               ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0             ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0                        
   
       
                             
            |
| 4 | | addcmpblnq0 6541 |
. . . . . . . . . . . . . . 15
        
   
       
   
       
                                         
                     ~Q0 ~Q0                        |
| 5 | 4 | imp 115 |
. . . . . . . . . . . . . 14
                     
   
       
                             
           
                     ~Q0 ~Q0                       |
| 6 | 3, 5 | syl 14 |
. . . . . . . . . . . . 13
             ~Q0 ~Q0            ~Q0 ~Q0               ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0             ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0                          ~Q0
~Q0                       |
| 7 | 2, 6 | erthi 6152 |
. . . . . . . . . . . 12
             ~Q0 ~Q0            ~Q0 ~Q0               ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0             ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0
~Q0                        ![] ]](rbrack.gif) ~Q0
~Q0  |
| 8 | | simprlr 490 |
. . . . . . . . . . . 12
             ~Q0 ~Q0            ~Q0 ~Q0               ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0             ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0                             ![] ]](rbrack.gif) ~Q0 ~Q0  |
| 9 | | simprrr 492 |
. . . . . . . . . . . 12
             ~Q0 ~Q0            ~Q0 ~Q0               ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0             ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0                             ![] ]](rbrack.gif) ~Q0 ~Q0  |
| 10 | 7, 8, 9 | 3eqtr4d 2082 |
. . . . . . . . . . 11
             ~Q0 ~Q0            ~Q0 ~Q0               ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0             ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0         |
| 11 | 10 | expr 357 |
. . . . . . . . . 10
             ~Q0 ~Q0            ~Q0 ~Q0              ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0               ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0        |
| 12 | 11 | exlimdvv 1777 |
. . . . . . . . 9
             ~Q0 ~Q0            ~Q0 ~Q0              ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                   ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0        |
| 13 | 12 | exlimdvv 1777 |
. . . . . . . 8
             ~Q0 ~Q0            ~Q0 ~Q0              ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                       ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0        |
| 14 | 13 | ex 108 |
. . . . . . 7
            ~Q0 ~Q0            ~Q0 ~Q0               ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                      ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0         |
| 15 | 14 | exlimdvv 1777 |
. . . . . 6
            ~Q0 ~Q0            ~Q0 ~Q0                   ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                      ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0         |
| 16 | 15 | exlimdvv 1777 |
. . . . 5
            ~Q0 ~Q0            ~Q0 ~Q0                       ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                      ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0         |
| 17 | 16 | impd 242 |
. . . 4
            ~Q0 ~Q0            ~Q0 ~Q0                        ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                     ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0   
     |
| 18 | 17 | alrimivv 1755 |
. . 3
            ~Q0 ~Q0            ~Q0 ~Q0                            ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                     ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0   
     |
| 19 | | opeq12 3551 |
. . . . . . . . . . 11
        
               |
| 20 | 19 | eceq1d 6142 |
. . . . . . . . . 10
        
         ![] ]](rbrack.gif) ~Q0 ~Q0        ![] ]](rbrack.gif) ~Q0 ~Q0  |
| 21 | 20 | eqeq2d 2051 |
. . . . . . . . 9
        
            ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   |
| 22 | 21 | anbi1d 438 |
. . . . . . . 8
        
             ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0            ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0    |
| 23 | | simpl 102 |
. . . . . . . . . . . . 13
        
       |
| 24 | 23 | oveq1d 5527 |
. . . . . . . . . . . 12
        
               |
| 25 | | simpr 103 |
. . . . . . . . . . . . 13
        
       |
| 26 | 25 | oveq1d 5527 |
. . . . . . . . . . . 12
        
               |
| 27 | 24, 26 | oveq12d 5530 |
. . . . . . . . . . 11
        
                               |
| 28 | 25 | oveq1d 5527 |
. . . . . . . . . . 11
        
               |
| 29 | 27, 28 | opeq12d 3557 |
. . . . . . . . . 10
        
                                               |
| 30 | 29 | eceq1d 6142 |
. . . . . . . . 9
        
                         ![] ]](rbrack.gif) ~Q0 ~Q0                        ![] ]](rbrack.gif) ~Q0 ~Q0  |
| 31 | 30 | eqeq2d 2051 |
. . . . . . . 8
        
                            ![] ]](rbrack.gif) ~Q0 ~Q0                          ![] ]](rbrack.gif) ~Q0 ~Q0   |
| 32 | 22, 31 | anbi12d 442 |
. . . . . . 7
        
              ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0             ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0    |
| 33 | | opeq12 3551 |
. . . . . . . . . . 11
        
               |
| 34 | 33 | eceq1d 6142 |
. . . . . . . . . 10
        
         ![] ]](rbrack.gif) ~Q0 ~Q0        ![] ]](rbrack.gif) ~Q0 ~Q0  |
| 35 | 34 | eqeq2d 2051 |
. . . . . . . . 9
        
            ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   |
| 36 | 35 | anbi2d 437 |
. . . . . . . 8
        
             ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0            ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0    |
| 37 | | simpr 103 |
. . . . . . . . . . . . 13
        
       |
| 38 | 37 | oveq2d 5528 |
. . . . . . . . . . . 12
        
               |
| 39 | | simpl 102 |
. . . . . . . . . . . . 13
        
       |
| 40 | 39 | oveq2d 5528 |
. . . . . . . . . . . 12
        
               |
| 41 | 38, 40 | oveq12d 5530 |
. . . . . . . . . . 11
        
                               |
| 42 | 37 | oveq2d 5528 |
. . . . . . . . . . 11
        
               |
| 43 | 41, 42 | opeq12d 3557 |
. . . . . . . . . 10
        
                                               |
| 44 | 43 | eceq1d 6142 |
. . . . . . . . 9
        
                         ![] ]](rbrack.gif) ~Q0 ~Q0                        ![] ]](rbrack.gif) ~Q0 ~Q0  |
| 45 | 44 | eqeq2d 2051 |
. . . . . . . 8
        
                            ![] ]](rbrack.gif) ~Q0 ~Q0                          ![] ]](rbrack.gif) ~Q0 ~Q0   |
| 46 | 36, 45 | anbi12d 442 |
. . . . . . 7
        
              ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0             ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0    |
| 47 | 32, 46 | cbvex4v 1805 |
. . . . . 6
                    ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                     ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0   |
| 48 | 47 | anbi2i 430 |
. . . . 5
                     ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                     ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                       ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                     ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0    |
| 49 | 48 | imbi1i 227 |
. . . 4
                      ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                     ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0   
    
                    ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                     ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0   
     |
| 50 | 49 | 2albii 1360 |
. . 3
                          ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                     ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0   
    
                        ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                     ![] ]](rbrack.gif) ~Q0
~Q0          ![] ]](rbrack.gif) ~Q0 ~Q0   
                       ![] ]](rbrack.gif) ~Q0 ~Q0   
     |
| 51 | 18, 50 | sylibr 137 |
. 2
            ~Q0 ~Q0            ~Q0 ~Q0                            ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                     ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0   
     |
| 52 | | eqeq1 2046 |
. . . . 5
                               ![] ]](rbrack.gif) ~Q0
~Q0                          ![] ]](rbrack.gif) ~Q0
~Q0   |
| 53 | 52 | anbi2d 437 |
. . . 4
                 ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0             ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0    |
| 54 | 53 | 4exbidv 1750 |
. . 3
                         ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                     ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0    |
| 55 | 54 | mo4 1961 |
. 2
  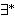                    ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0                     ![] ]](rbrack.gif) ~Q0 ~Q0  
       ![] ]](rbrack.gif) ~Q0 ~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0   
     |
| 56 | 51, 55 | sylibr 137 |
1
            ~Q0 ~Q0            ~Q0 ~Q0    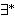                    ![] ]](rbrack.gif) ~Q0 ~Q0          ![] ]](rbrack.gif) ~Q0
~Q0                           ![] ]](rbrack.gif) ~Q0 ~Q0   |